들어가며
GeoHash에 이어 알아볼 그리드(Raster) 시스템은 Uber에서 개발한 H3다.
앞서 말했듯이 그리드 시스템을 사용하면 지리 공간적 데이터를 효율적으로 분석하여 셀(Cell)을 통해 지리 공간적 클러스터를 만들 수 있다.
그리드 시스템은 지리 공간적 데이터를 쉽고 효율적으로 집계, 클러스터, 분할, 축소, 조인 및 인덱싱할 수 있다.
이를 통해 쿼리 런타임 성능을 향상시키고, 저장된 데이터 크기를 줄일 수도 있다.
대표적인 그리드 시스템으로 GeoHash, S2, H3등이 있다.
이번 글은 Uber에서 개발한 H3가 무엇이며, 왜 우버가 H3를 만들었는지 살펴본다.
그리고 H3의 특징에 대해서 살펴본다.
1 H3
가장 먼저 알아 볼 부분은 H3의 개념과 특징이다.
1-1 H3란?
H3는 Geo-Hash와 유사한 전세계 지도를 육각형 셀로 분할하는 지리 공간 인덱싱 시스템이다.
H3는 Uber에의해 만들어졌으며, 현재는 Apache 2 라이센스하에 오픈소스로 되어있다.
H3는 아래와 같이 다양한 기능을 제공한다.
- 위경도를 H3셀로 변환할 수 있다.
- H3셀의 중심 위경도를 찾을 수 있다.
- H3셀의 경계(Boundary) 좌표를 구할 수 있다.
- H3셀의 이웃을 찾을 수 있다.
아마 이전 Geo-Hash 글을 보고온 사람이라면 위 기능들은 H3뿐만 아니라 기타 Grid 시스템도 제공해준다는 것을 눈치챘을 것이다.
1-2 H3는 Grid 시스템이며, Grid 시스템은 인덱싱이 핵심이다
이전 Geo-Hash 글에서 이야기했듯이, 위경도는 실제 정확한 위치를 측정하는 것이 목표여서 무한하게 표현되기때문에 특정 영역 (Area)에 대한 처리를 하기엔 부적합하다.
그리고 공간에 대한 처리를 더 효율적으로 하기위해 만들어진 것이 바로 Grid 시스템이다.
Grid 시스템의 핵심은 바로 인덱싱이다. 즉, 지구의 특정 지역을 일정한 크기대로 인덱싱하여 공간 처리에 대한 효율을 높이는 것이다.
💁♂️ Geo-Hash로 알아보는 그리드 시스템의 인덱싱
Grid 시스템의 가장 초기 시스템격인 Geo-Hash는 말그대로 hash 함수를 이용한다.
hash 함수의 핵심은 특정 데이터를 찾을 때 하나하나 비교하며 찾는 것보다 해시 키를 계산하여 그 키에 해당하는 장소를 바로 찾는 것이다. O(1)의 시간복잡도
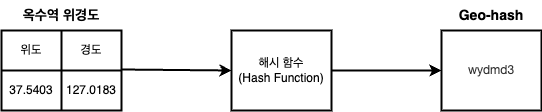
`위경도 -> Hash -> Geo-Hash`로 변환되는 과정
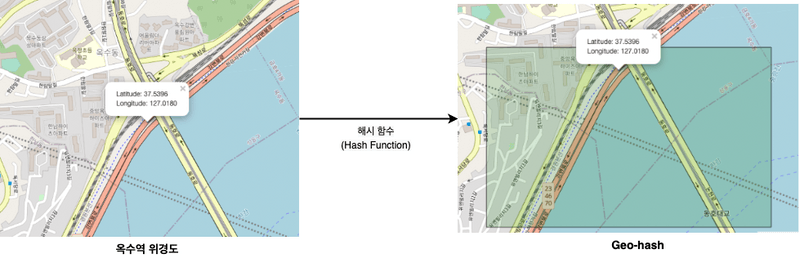
특정 Hash 함수를 이용하여 위경도를 특정 공간을 나타내는 공간으로 인덱싱한다.
쉽게 말해, Geo-Hash는 특정 해시 함수를 이용하여 공간 상의 위경도 좌표값을 일정한 값으로 치환하는 것을 의미한다.
그리고 이를 통해 전 지구를 특정 크기의 정사각형으로 인덱싱함으로써 공간 처리에 대한 효율을 높인다.
💁♂️ H3도 Geo-Hash와 동일하게 인덱싱한다.
H3도 위에서 말한 Geo-Hash와 별반 다르지않다. 동일하게 위경도를 H3의 해시 함수를 통해 H3 셀로 변환하여 인덱싱한다.
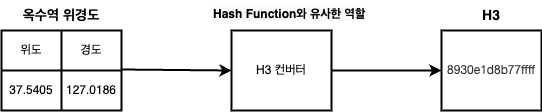
`위경도 -> H3 컨버터 -> H3`로 변환되는 과정
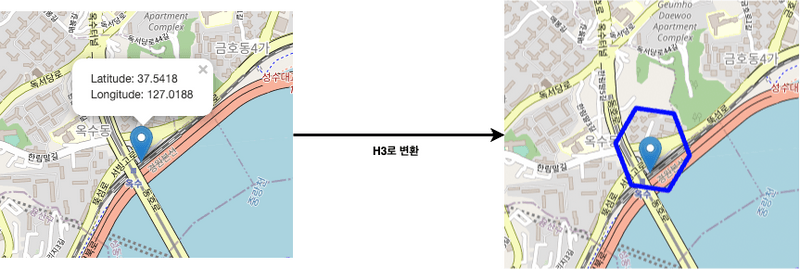
위경도를 H3로 변환하여 특정 공간을 나타내는 공간으로 인덱싱한다.
쉽게 말해, H3도 Geo-Hash와 동일하게 특정 함수를 이용하여 공간 상의 위경도 좌표값을 일정한 값으로 치환한다.
그리고 이를 통해 전 지구를 육각형으로 인덱싱함으로써 공간 처리에 대한 효율을 높인다.
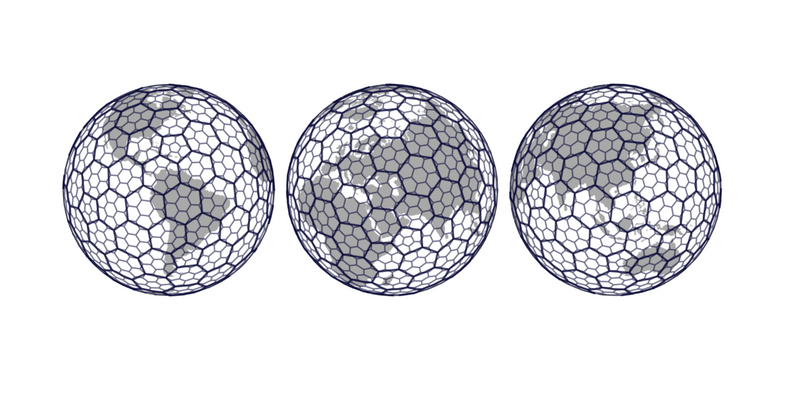
지구를 H3셀로 인덱싱한 결과
1-3 Uber가 H3를 만든 이유
이 부분은 내가 개인적으로 궁금하여 정리한 내용이다. PIP를 사용하는데 필요한 내용은 아니므로 스킵해도 무방하다.
Geo-Hash와 같은 Grid 시스템이 이미 존재하는데도, 우버는 왜 H3라는 새로운 Grid 시스템을 만든 것일까?
그 이유는 Uber의 발표를 통해 알 수 있다.
- 우버의 최종목표는 사용자가 요청할 때 배차해야할 차를 무조건 존재하게하는 것이다.
- 예를 들어, 스포츠 경기, 콘서트등 이벤트가 종료되고나서 많은 배차 요청이오는데, 이때 차가 부족하여 배차를 못받는 경우가 없도록하기위함이다.
- 우버의 목표를 만족시키는 방법 -> 드라이버의 공급을 늘려야한다.
- 드라이버의 공급을 늘리기위해 사용된 방법이 바로 Surge Price (가격 인상)이다.
- 이는 특정 지역의 수요가 많아지면, 해당 지역을 가격 인상 지역으로 설정하여 추가 요금을 받고 배차를 생성해주는 방식이다.
- Surge Price (가격 인상) 방식도 문제는 존재한다.
- Surge Trip
- 가장 큰 문제는 드라이버가 Surge Price 지역만을 찾아다니게된다는 것이다. (이를 Surge Trip이라고 부른다.)
- 이로인해 Surge Price 지역이 아니라면 배차가 잘 생기지않고, 취소가 많아져 전체적인 마켓에 악영향을 끼치게된다.
- 유령 수요
- 또 다른 문제는 우버는 기본적으로 인근 몇 K/M내의 요청을 받아 배차를 생성하는데, Surge Price가 해당 K/M의 버위를 벗어남에따라 유령 수요가 많이 발생하게되었다고한다.
- 즉, Surge Price 범위내에서도 고객의 요청이 드라이버에게까지 가지못하는 경우가 많이 발생했다. (초기에 우버는 도시단위로 Surge Price를 형성하였다고한다.. 굉장히 큰 범위라고 볼 수 있다.)
- 이를 Pantom Demand (유령 수요)라고 부르며, Surge Price 지역이 너무 넓어서 발생하는 문제라고볼 수 있다.
- Surge Trip
- Surge Price (가격 인상)에서 발생하는 문제를 해결하는 방법은 Grid System을 이용하여 여러 크기의 셀에서의 사용자 Action을 모두 인지하고 대처하는 것이다.
- 그리하여 아래와 같은 우버의 요구사항에 맞게 Grid System인 H3를 만들어 사용하게되었다고한다.
- Smooth gradients of demand를 구현할 수 있음
- 동적으로 특정 셀의 변화도를 측정할 수 있다. (사용자의 배차요청수를 동적으로 계속해서 측정할 수 있다.) ex. 교통량 측정
- Clear center of demand
- Dynamic neighborhoods
- Smooth gradients of demand를 구현할 수 있음
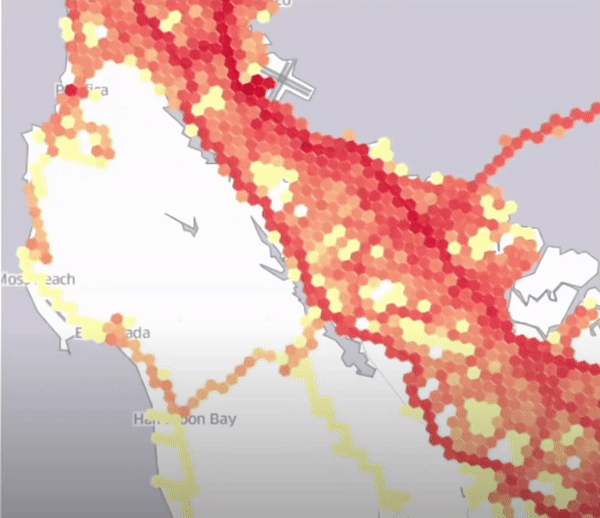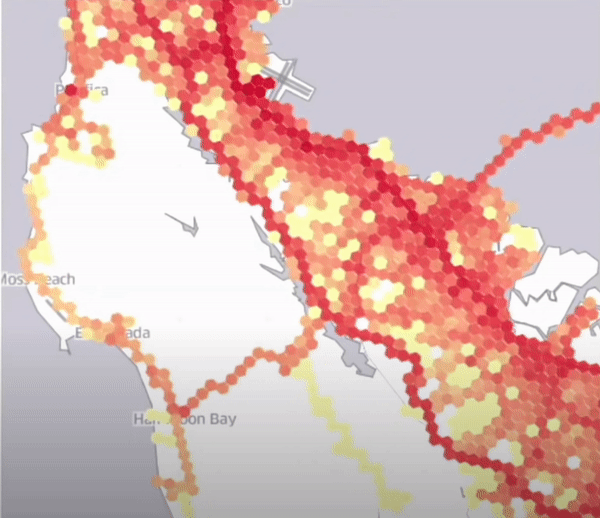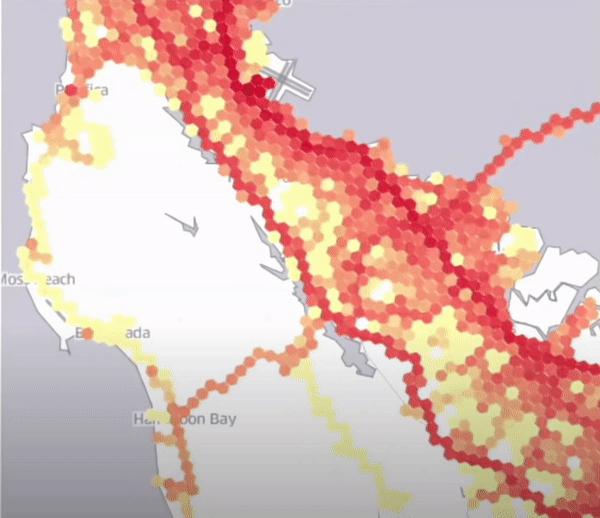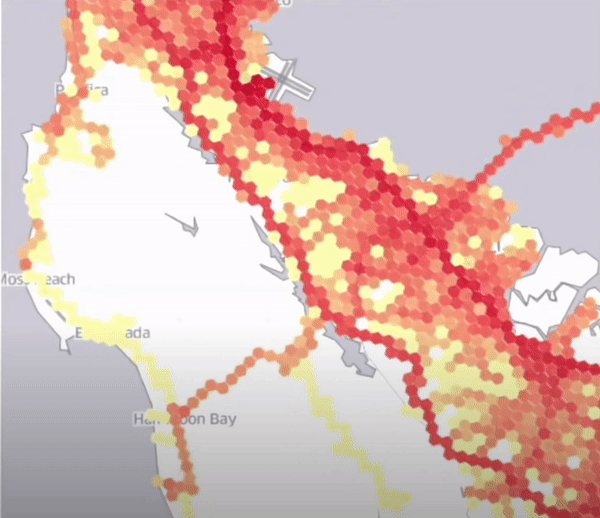
H3를 이용하여 동적으로 셀의 변화도를 시각화한 결과 (셀별로 동적 가격 정책을 다르게 할 수 있다.)
1-4 왜 육각형인가?
H3와 Geo-Hash 모두 그리드 시스템이며, 지구를 특정 규격의 일정한 크기로 클러스터링하여 공간 처리를 효율화시켰다고보면된다.
하지만 H3는 정사각형인 Geo-Hash와 다르게 육각형으로 공간을 클러스터링한다.
🤔 왜 육각형일까?
1️⃣ Neighbors Traversal - 육각형끼리의 거리가 동일하다.
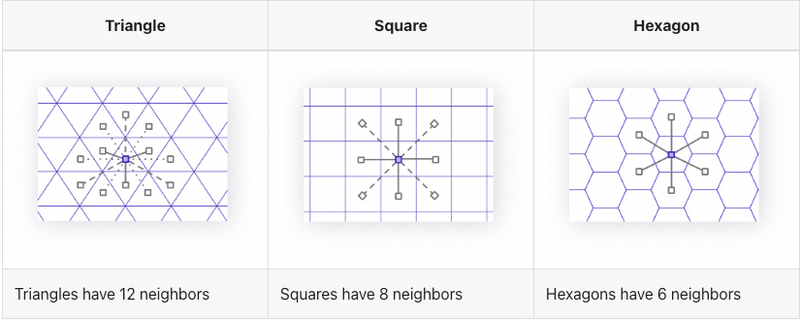
출처: https://h3geo.org/docs/highlights/aggregation
위 그림에서 볼 수 있듯이, 삼각형과 사각형은 인근 셀과의 좌우상하과 대각선의 거리가 모두 다르다.
반면에 H3는 좌우상하와 대각선의 거리가 모두 동일하다.
즉, 인접하고있는 셀로 이동할 때 어떠한 방향과 각도로 이동하든 각 셀의 중심점까지의 거리가 동일하다.
Uber가 H3를 만들게된 계기도 차량 배치에 대한 정확도와 배치 가격을 정확히 측정하려고했다고하는데, 아마 이러한 부분에서 셀간의 거리가 같은 것이 계산이 효율적이고 일정해서 그런게 아닌가 싶다.
2️⃣ 평균적으로 사각형보다 육각형이 더 작은 오차 범위로 Polygon (다각형)공간을 셀로 채울 수 있다.
출처: https://h3geo.org/docs/highlights/aggregation
육각형은 특정 Polygon을 채우는데 가장 최적의 도형이라고한다.
그리고 H3의 공식문서에서 평균적으로 사각형보다 육각형이 더 작은 오차 범위로 Polygon (다각형)공간을 셀로 채울 수 있다고 말한다.
물론 검증이 필요한 부분이기도하다.
3️⃣ 육각형은 Distortion(왜곡)없이 지구를 Projection (투영)할 수 있다.
지구는 Sphere (구체)이므로 평평하지않다. 그러나 Grid System은 평평하게 공간을 분석한다.
그러므로 지구를 Grid System으로 Projection (투영)해야 사용 및 분석할 수 있다.
구체를 평평하게 Projection하면 어쩔 수 없이 왜곡이 발생하게된다. H3는 이러한 왜곡을 최소화하는 Polygon이 육각형이라고 판단되어 채택했다고한다.
실제로 가장 중요한 이유였다고하며, 다양한 Projection 방법중에 H3는 DYMAXION 방법을 채택했다고한다.
❗️ 물론 단점으로 H3는 세분화 및 재조합(subdivision)이 완벽하지않다는 것이다. - 중요
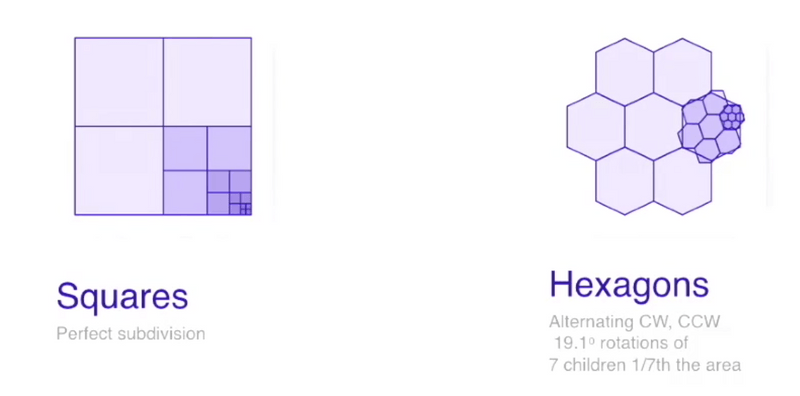
출처: https://www.youtube.com/watch?v=ay2uwtRO3QE
위 그림을 보면 알 수 있듯이, 모든 H3셀은 7개의 자식을 가지게되지만, Geo-Hash의 정사각형에 비해 육각형은 계층간의 완벽히 분리 및 재조합되진않는다.
하지만 부모와 자식간의 변환이 일정하므로 H3 인덱스의 고정 오차 범위 내에서 정밀도를 만족할 수 있다고한다.
이와 관련된 더 자세한 내용은 공식 문서를 참고.
1-5 H3 특징
H3의 기본적인 개념을 이해했다면, 이제 H3의 특징에 대해서 알아본다.
Grid 시스템의 특징이자 H3의 특징을 정리하였다.
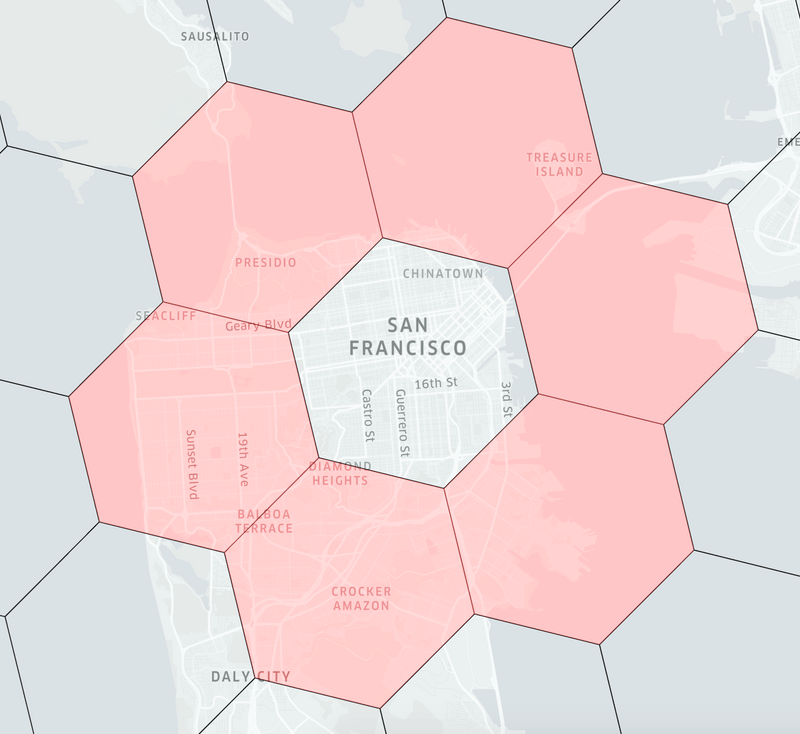
💁♂️ H3의 단위는 점 (Point)가 아닌 셀 (cell)이다.
셀이란 특정 범위의 공간(Area)을 의미한다.
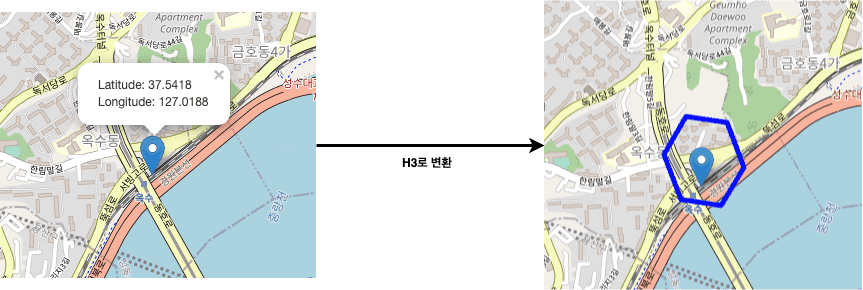
그리고 아래와 같이 옥수역 부근의 위경도를 H3 셀로 변환하면 모두 동일한 H3셀 값이 나오게된다.
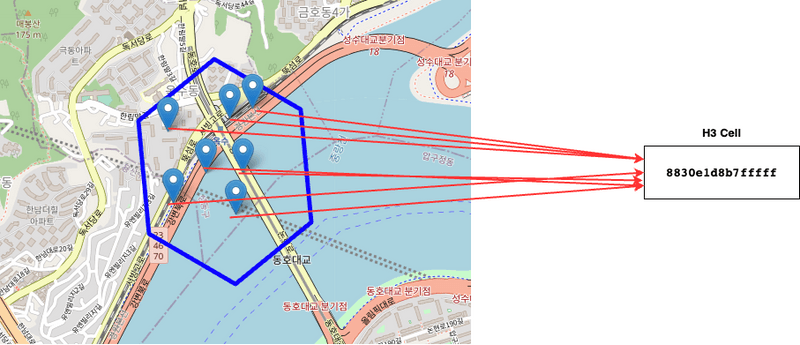
위 그림과 같이 옥수역 부근의 H3 셀 안의 존재하는 위경도를 H3로 변환하면 모두 동일하게 8830e1d8b7fffff가 나오는 것을 볼 수 있다.
즉, H3의 단위는 점이 아닌 지구를 인덱싱한 공간 (Area)이다.
그러기에 정확한 위치를 특정할 순 없지만, 공간을 찾거나 처리하는데 있어서 훨씬 비용이 적고 효율적이다.
물론 Resolution이 높으면 비교적 정확한 위치를 특정할 수 있다. 단, 이렇게 할 경우 처리량이 증가하게된다.
💁♂️ H3의 목적은 계층적 구조를 통해 연산량을 줄이는 것이라고 볼 수 있다.
위경도는 실제 정확한 위치를 측정할 수 있다는 장점이 있다. 하지만 무한하게 표현되기때문에 특정 공간에 대한 처리를 하는데는 부적합하다.
반면에, H3는 실제 완전 정확한 위치를 측정할 수는 없지만, 유한하게 표현되며 인덱스 비슷하게 동작하기에 공간에 대한 처리를하는데 적합하다고 볼 수 있다.
이를 풀어말하면, H3도 Geo-Hash와 동일하게 결국 모자이크 처리라고 볼 수 있다.
Grid 시스템의 특징이라고 볼 수 있다.

Geo-Hash를 통해 살펴보는 모자이크
이미지로 비유해보면 가장 선명한 이미지가 위경도(GPS)이고, H3의 Resolution (해상도)가 낮아질수록 이미지를 알아보기 힘들어진다.
이를 공간 좌표로 대입해본다면 위경도는 정확한 위치를 특정할 수 있지만, 무한하게 표현되기에 특정 공간을 찾는데 비용이크다.
반면에, H3는 정확한 위치를 특정하기 어렵지만, 유한하게 표현되기에 굉장히 적은 연산량으로 특정 공간을 찾거나 처리할 수 있다.
쉽게 생각해봐도, 픽셀이 촘촘히 많아 무한한 범위안에서 특정 조건에 맞는 점이나 공간을 찾는 것은 모든 범위를 탐색해야하는 문제가 있다.
위경도는 심지어 소수점까지있기에 거의 무한하다고볼 수 있다.
반면에, 모자이크와 같이 픽셀을 낮출수록, 픽셀량이 적어지기에 탐색해야하는 범위가 점점 줄어들게된다.
이를 통해 연산량을 크게 줄일 수 있다. 이 부분이 바로 H3와 기타 Grid 시스템의 핵심이라고 볼 수 있다.
💁♂️ H3는 공간을 탐색하는데 용이한 반면 오차 범위가 존재한다.
H3의 레벨별 셀의 실제 크기는 아래와 같다.
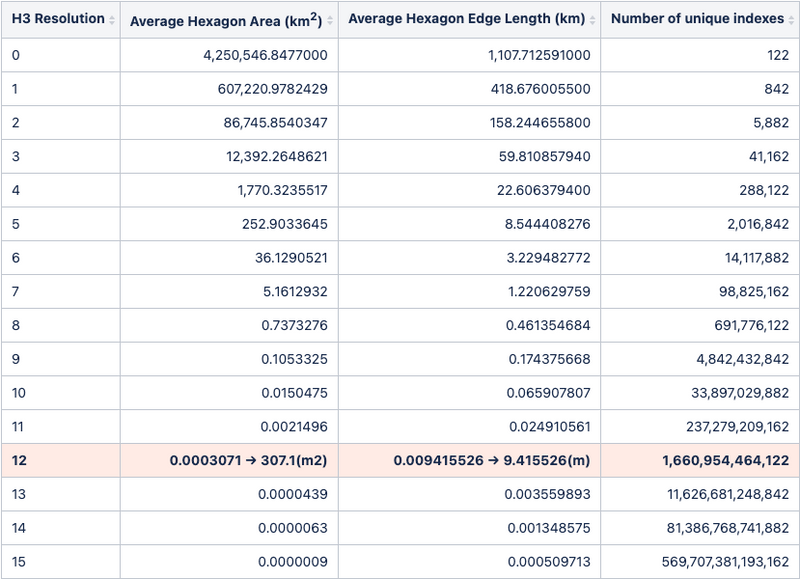
참고: https://h3geo.org/docs/core-library/restable
당연히 H3도 기타 Grid 시스템과 동일하게 특정 점을 나타내지않고, 공간 (Area)를 표기하기때문에 조금의 오차가 존재한다.
Resolution (해상도)가 높아질수록 육각형이 더 작아지고 표기하고자하는 점에 대한 오차는 점점 줄어들게된다.
단, Resolution이 높아질수록 처리해야할 H3 셀이 많아지기때문에 연산에 대한 성능이 떨어지게된다.
💁♂️ 이웃 셀을 쉽게 찾을 수 있다.
기존의 벡터에 위경도를 투영하는 방식은 특정 Polygon의 이웃 Polygon을 찾기 쉽지않다.
H3는 알고리즘 특성상 쉽고 빠르게 이웃 셀을 판별하고 찾을 수 있다.
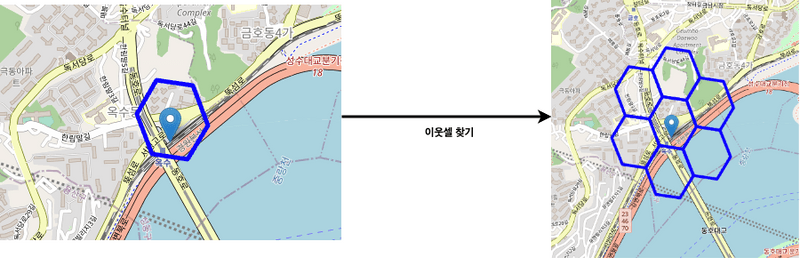
H3 이웃셀 찾기
2 H3 인덱싱 알고리즘
H3는 어떻게 지구를 육각형으로 일정하게 인덱싱하며, 위경도를 H3셀로 변환하는 것일까?
정확한 변환 과정은 추후에 더 알아보고 정리할 계획이다.. 우선은 아래 참고 자료를 살펴보길 추천한다.
3 Python을 이용한 H3 학습테스트
H3에 대한 개념과 특징에 대해서 어느정도 이해했다면, 이제 파이썬을 이용하여 이를 직접 구현해본다.
학습 테스트에 대한 모든 코드와 설명은 다른 글 - H3 학습테스트에 정리해두었다.
위 학습 테스트를 따라하며 H3가 어떻게 동작하며, 어떻게 사용하는지 자세히 살펴보길 추천한다.